Enhancing Embedding Separation with ArcFace Loss
Embeddings play a crucial role in Machine Learning by capturing and representing relationships between objects.
Embeddings can be obtained from Neural Networks trained with traditional classification losses. However, these losses do not explicitly optimize cosine distances to achieve both inter-class separability and intra-class compactness.
In this article, we will delve into ArcFace loss and its suitability for tasks that require high degree of inter-class separability while still having high intra-class variance, such as face recognition.
Embeddings & Separability
Before we start discussing losses, let’s take a refresher on what embeddings are:
- Embeddings are mathematical representations of objects in a vector space.
- They can usually be obtained by training a Neural Network.
- Similar objects have embeddings that are close to each other.
- The similarity is measured using distance metrics like euclidean or cosine distance.
- We usually want embeddings such that objects belonging to the same class are close together whereas objects belonging to different classes are further apart.
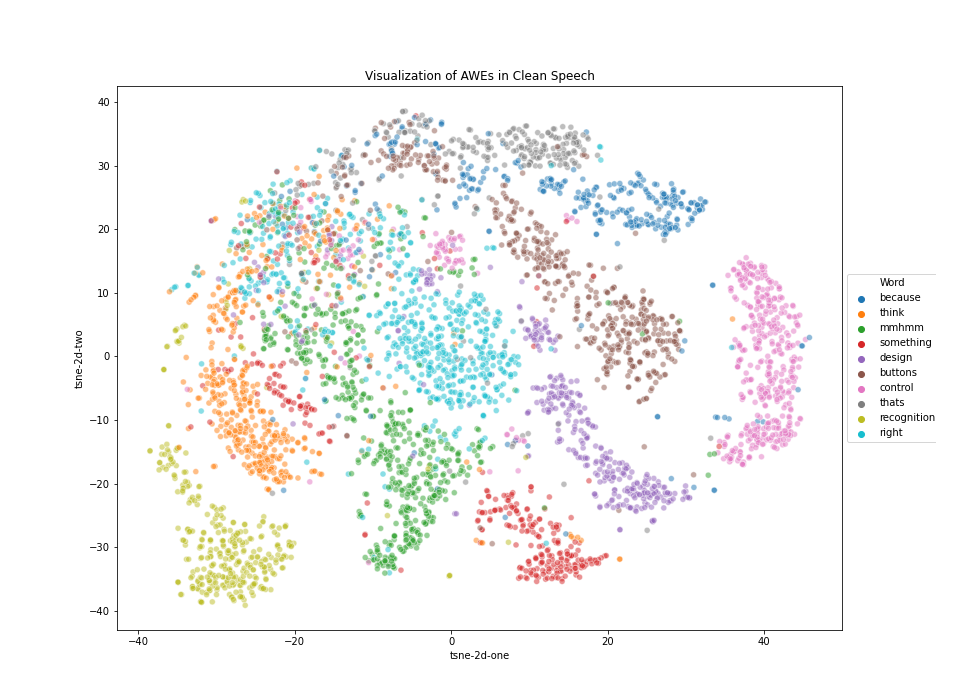
Source: Study of Acoustic Word Embeddings in relation to Mishearing of Words, Jayesh Mahapatra 2021
Embedding separation with Softmax Loss
Classical Softmax Loss looks like this
\[L_{1} = -log \frac{e^{W^T_{y_i}x_i + b_{y_i}}}{\sum^N_{j=1}e^{W^T_jx_i + b_j}}\]Let’s break down the equation to understand the individual elements:
- Features: $x_i \in \mathbb{R}^d$ represents features of $i$-th example of the $y$-th class.
- Weights: $W_j \in \mathbb{R}^d$ is the $j$-th column of weight matrix $W \in \mathbb{R}^{d \times N}$.
- Bias: $b_j \in \mathbb{R}^N$ is the bias term.
- Number of Classes: $N$ denotes the number of unique classes in the dataset.
Since we are not constraining the weight matrix $W$ or the features $x_i$ in anyway, the loss function does not explicitly consider the angular relationship between embeddings. This means that optimizing for this loss doesn’t explicitly promote angular separibility of embeddings belonging to different classes, neither does it explicitly enforce intra-class angular similarity.
ArcFace Loss
Let’s now modify the softmax loss to explicitly care about the angles between embeddings.
For simplicity we can set the bias term $b_j = 0$. Then we can rewrite $W^T_jx_i = \Vert W_j \Vert \Vert x_i \Vert cos \theta_j $ , where $\theta_j$ is the angle between the weight $W_j$ and feature $x_j$.
Our goal is to modify the loss function such that the predictions only depend on $\theta_j$.
We can achieve this by normalizing the other two terms in the equation:
- We set $\Vert W_j \Vert = 1$ using $l_2$ normalization
- We normalize features $ \Vert x_i \Vert $ by $l_2$ normalization and re-scale it by $s$.
Following these modifications the loss function becomes:
\[L_2 = -log \frac{e^{s\cos \theta_{y_i}}}{e^{s\cos \theta_{y_i}} + \sum^{N}_{j=1,j\neq y_i} e^{s \cos \theta_j}}\]Now the predictions only depend on $\theta$, and the features are distributed on a hypersphere with radius $s$. The scaling parameter $s$ is used to control the overall range of output logits which in term affects how large the gradients will be during training.
We can improve this further by introducing an additive angular margin parameter $m$ to the angle $\theta$ between $W_{y_i}$ and $x_i$. A margin encourages better class separation by penalizing the loss function if examples fall within a certain distance from the decision boundary. In our case, since we are using angular distances, our margin $m$ is also angular.
The final loss then becomes:
\[L_3 = -log \frac{e^{s \cos (\theta_{y_i} + m) }}{e^{s\cos (\theta_{y_i} + m)} + \sum^{N}_{j=1,j\neq y_i} e^{s \cos \theta_j}}\]This is the ArcFace Loss that is widely used in training face recognition systems.
Experimental Results
In order to demonstrate the difference in class separation when using arcface loss vs classic softmax, I have created a github repository called ArcFace-Embedding-Visualization.
This repository contains contains code for visualizing how embeddings evolve when trained using ArcFace vs Softmax Loss, as shown below:
Visualization of Embedding Separation across Training Epochs
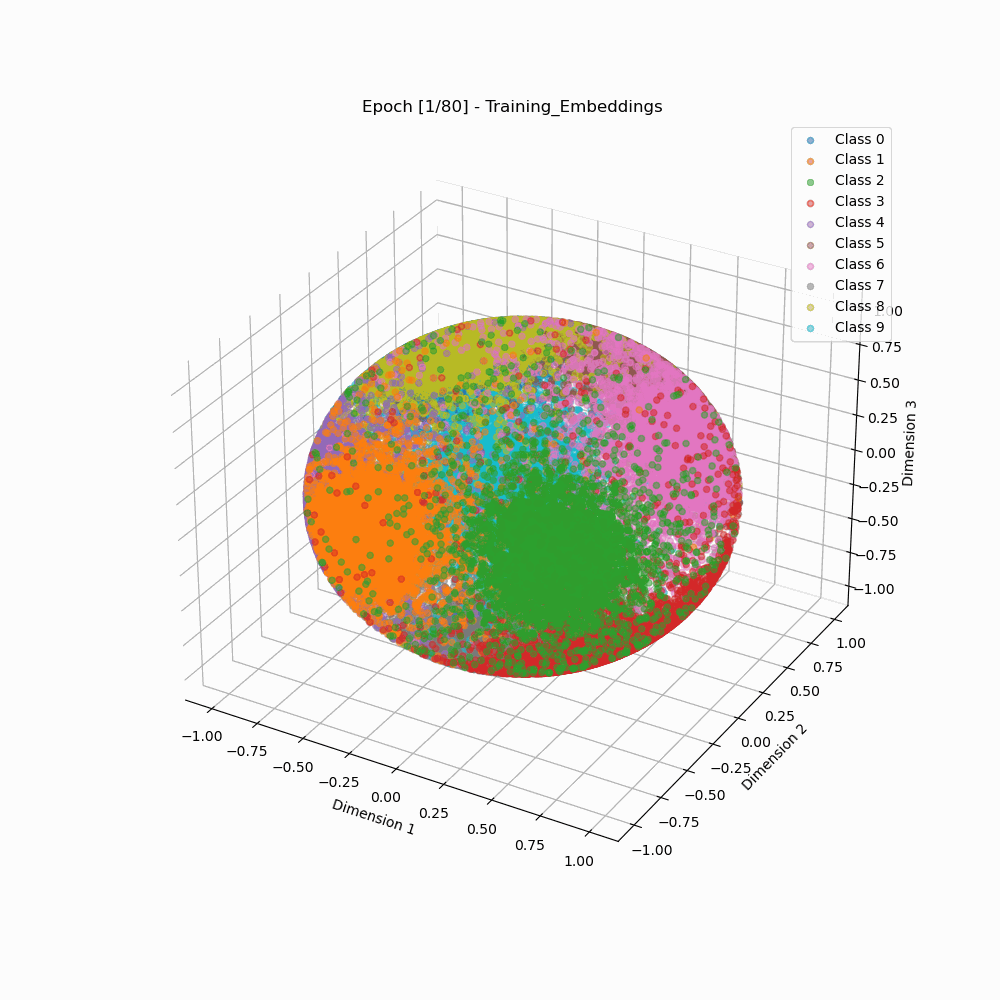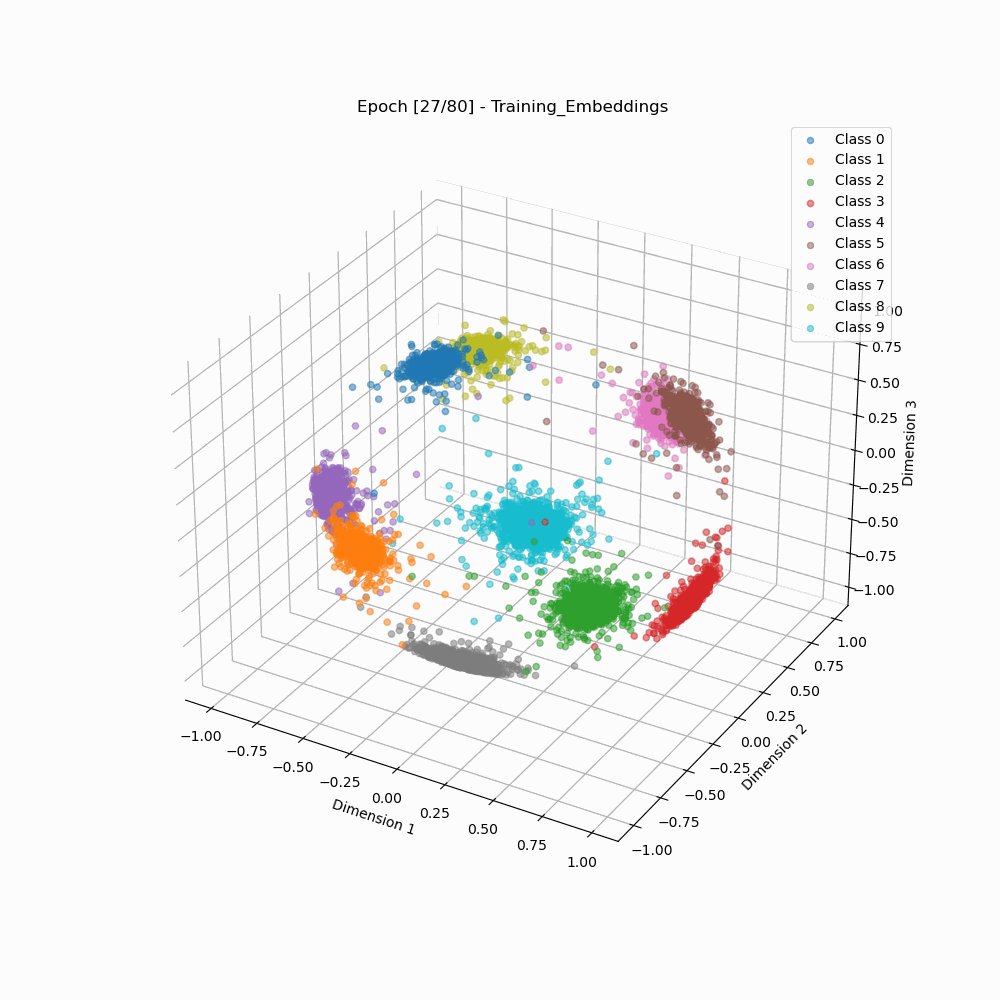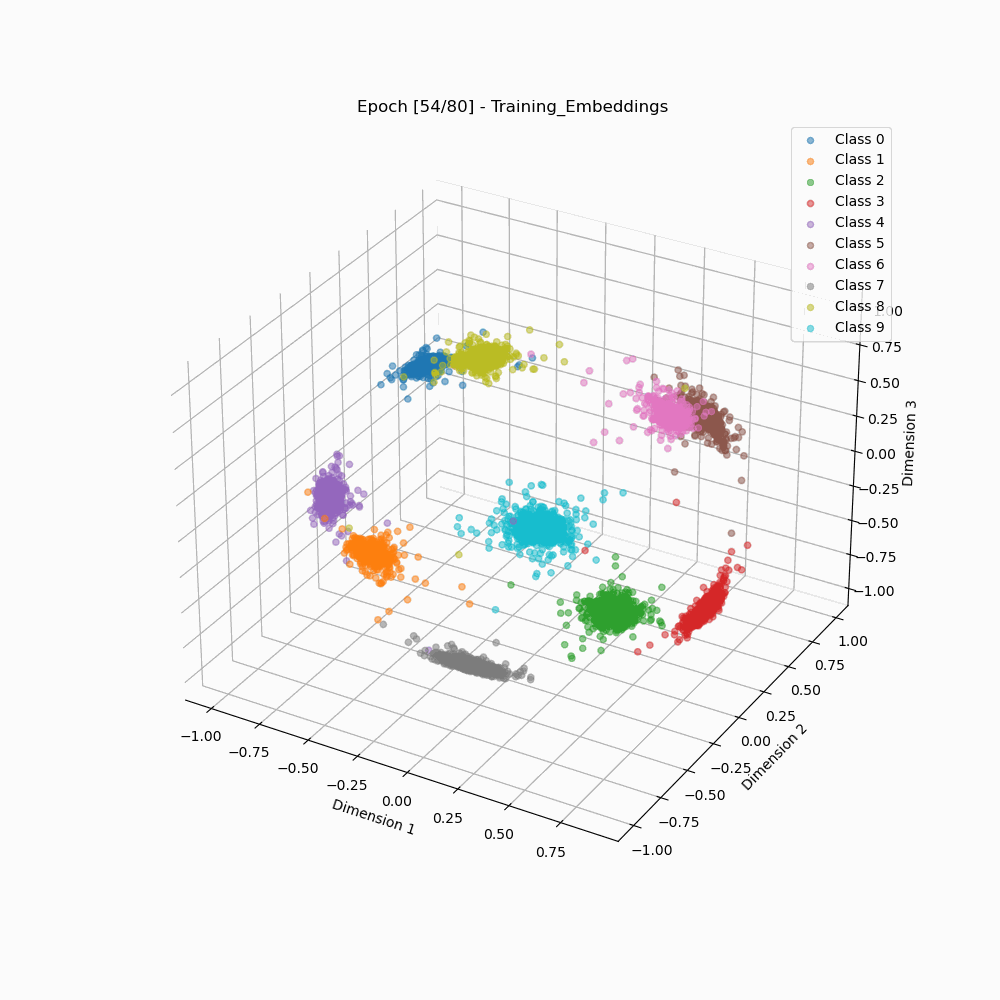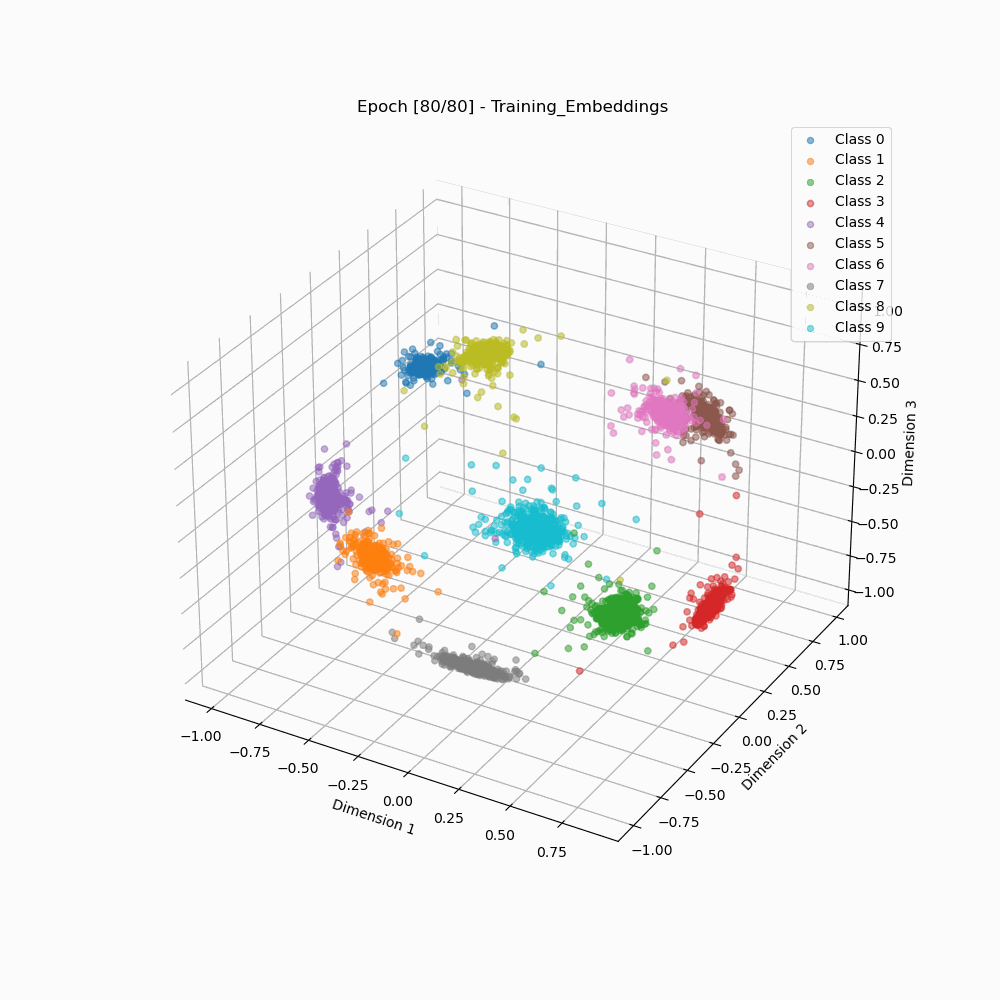
ArcFace 3D embeddings during training. |
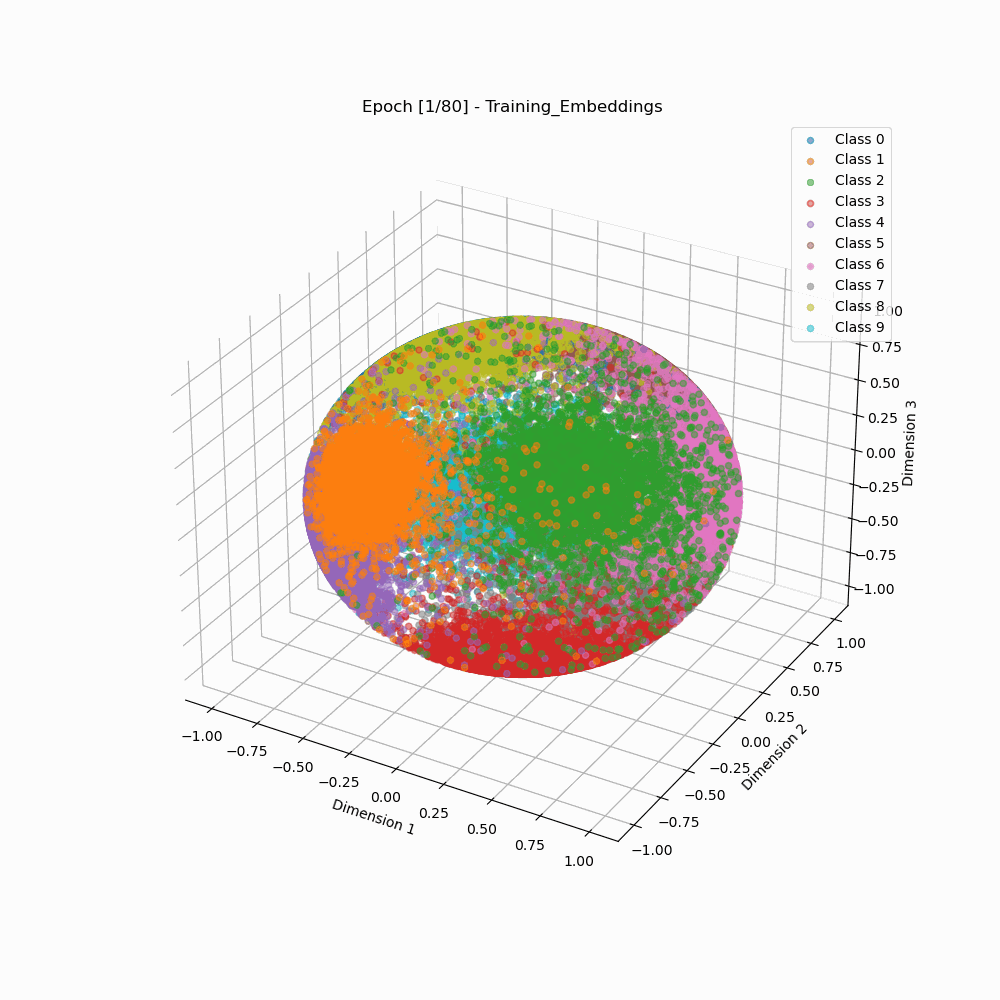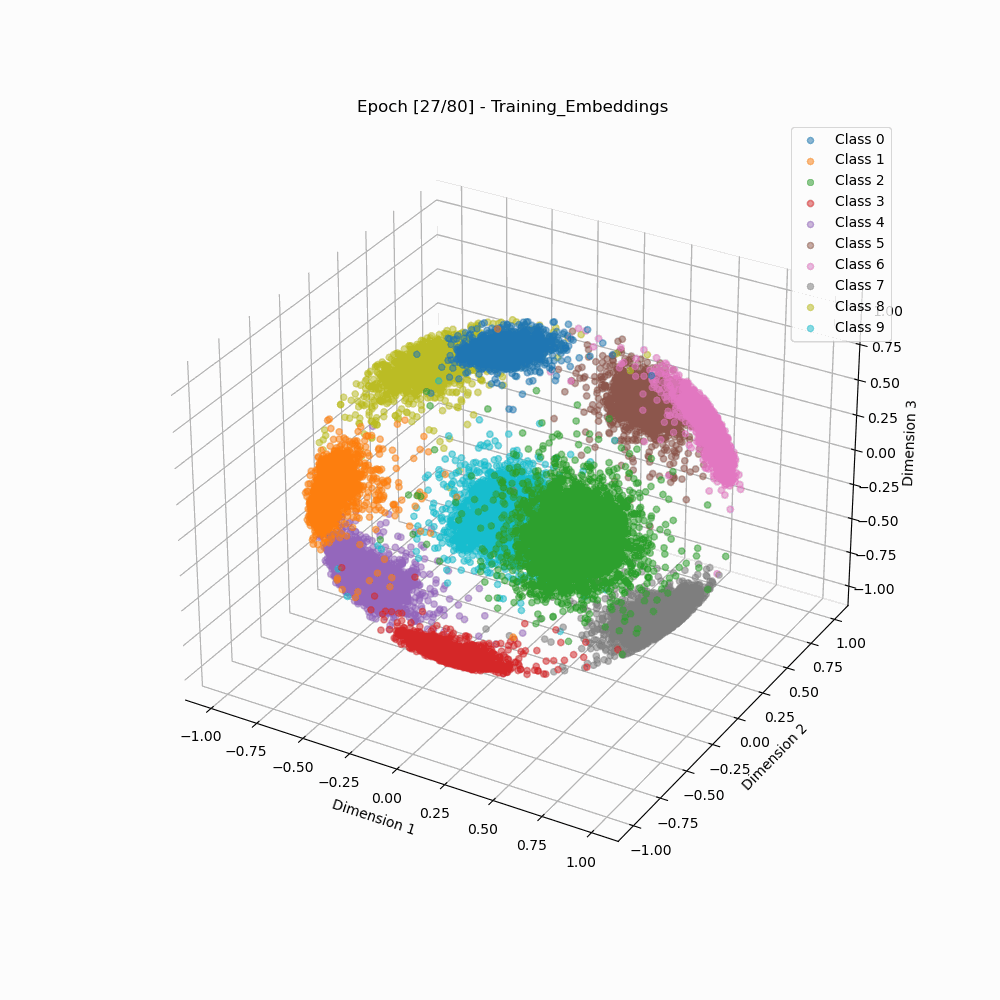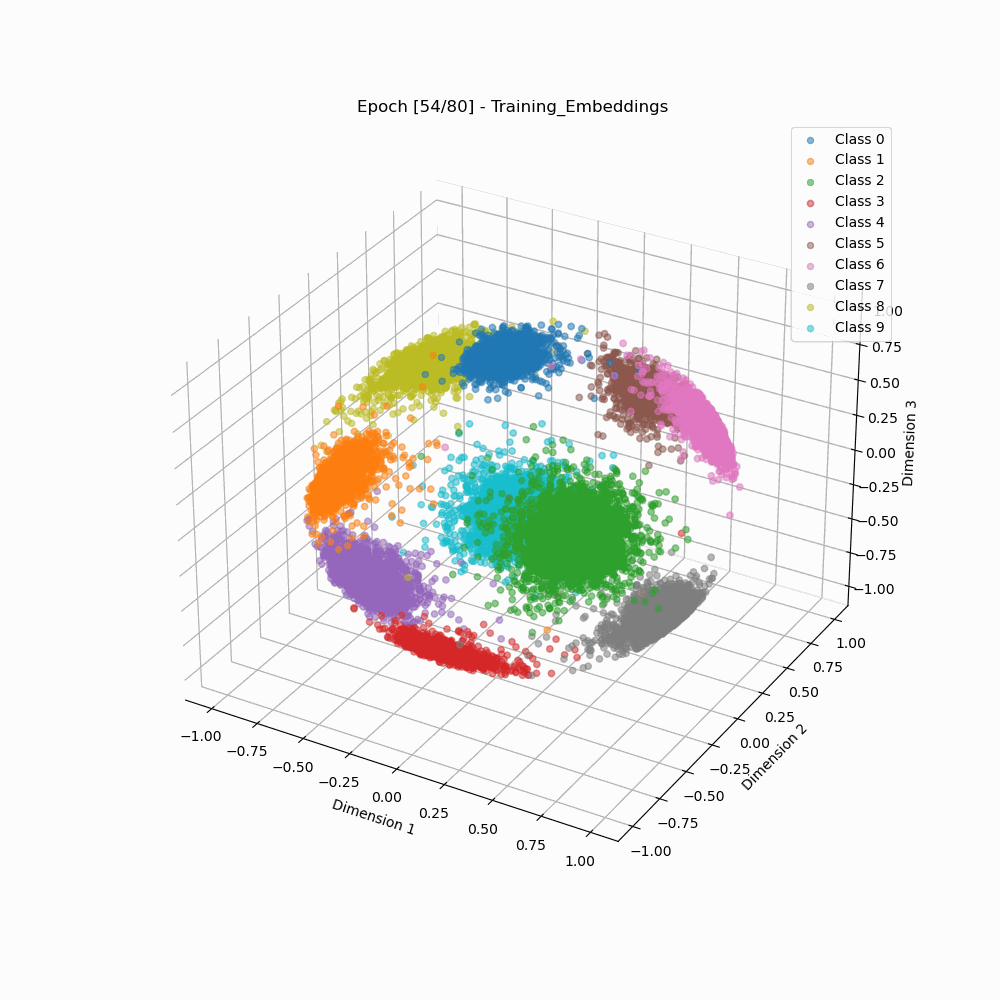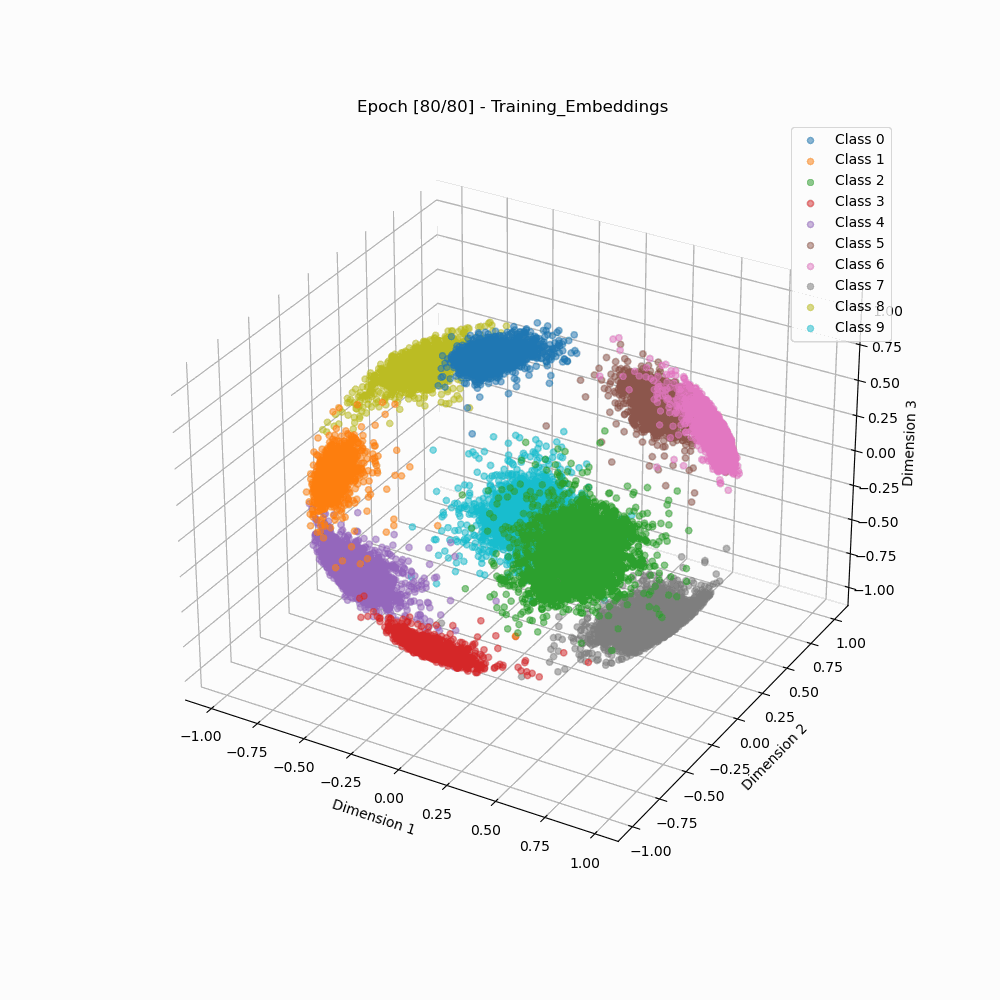
Softmax 3D embeddings during training. |
As we can see that the arcface loss results in embedding clusters that are more cleanly separated as well as are more compact than the embeddings trained using classic softmax.
The provided code trains a VGG8 network on the popular MNIST dataset using the ArcFace loss and Softmax loss, and generates visualization of embeddings. For more information on how to create and visualize such embeddings, please checkout the repository.
Conclusion
In conclusion, in this blog post we introduced ArcFace loss as a powerful technique for achieving enhanced embedding separability. By explicitly considering the angles between embeddings, ArcFace loss provides improved discrimination of embeddings, especially in face recognition tasks.